
Mtext("U:/efg/lab/R/MixturesOfDistributions/TwoGaussians.R", # Only keep the first four the correpsond to four s.approx values # Approximate location of mean of normal distribution: Valleys.Deriv2 <- peaks(-derivative2$y, span=3) Peaks.Deriv2 <- peaks( derivative2$y, span=3) Plot(derivative2$x,derivative2$y, type="l", S.approx <- (derivative1$x - derivative1$x)/2 # Approximate location of peak and valley Valleys.Deriv1 <- peaks(-derivative1$y, span=3) Peaks.Deriv1 <- peaks( derivative1$y, span=3) Plot(derivative1$x,derivative1$y, type="l", # According to Abramowitz & Stegun, inflection points are at +/- sigma.
Range <- 2:(length(x)-1) # Drop first and last points Spacing of x-points assumed to be uniform. # Spacing of x-points need not be uniform Adjust x values to be center of interval. V <- max.col(z, "first") = 1 + s # take first if a tie # (see efg's posting to R-Help on about problem with ties.) # integrate(P,-5,5, mean=0, sd=1) # should be close to 1.0

# distribution), but other functions could be tried here.Įxp(-(x-mean)^2/(2*variance)) / sqrt(2*pi*variance) # Here P is the same as dnorm (probability density function for normal I found something interesting searching for the sum of two gaussians and nonlinear models (nls). Also, final tip: if you want to see the optimal final parameter estimates selected by nls(), just type summary(fit) (substituting, if necessary, whatever alternative object variable name you may have chosen in place of fit, to hold the fit information). I chose algorithm="port" in order to mitigate this problem somewhat. In particular, the default Gauss-Newton fit algorithm can be especially fussy about good starting values, and may even return a "singular gradient" error (which appears to be distinct, as an error condition, from convergence failure). If they aren't at least reasonably close to the correct search neighborhood, you can end up with convergence failures. Please beware that nls() can be somewhat fussy about having good starting parameter values. Geom_smooth(data=dffit, stat="identity", color="red", size=1.5)) Print(ggplot(df, aes(x=Tiempo, y=UT4)) + geom_point() + # Plot the data with the model superimposed # Predict the fitted model to a denser grid of x valuesĭffit <- ame(Tiempo=seq(616.2, 621.8, 0.01)) # of fussy about choosing "reasonable" starting guesses for the parameters. # Fit to a model consisting of a pair of Gaussians. To fit two Gaussians, you may use the nls() function, as in the following example: library(ggplot2) So unfortunately, I suspect that my answer has probably become somewhat stale news by this point, but I'll still post it anyhow, just in case it may still be of some small use to somebody. Despite my emphatic protests to the moderators, the "on hold" status was allowed to simply languish for a week without any further attention, only to be closed ultimately without comment or explanation. I had originally intended to post my solution a week ago, on the main site, back when this question was first posed over there, however the version which appeared in that forum was placed on hold while I was actually in the midst of entering my solution. I hope I've made myself clear with the question. I've found some ideas here using ksmooth fitting multiple peaks to a dataset and extracting individual peak information in R, but the result I got was a unimodal fit of my data. My goal is to fit a multi-peak Gaussian of every column UT$_i$ in order to get the parameters for a generic UT and use it for a further statistical analysis.
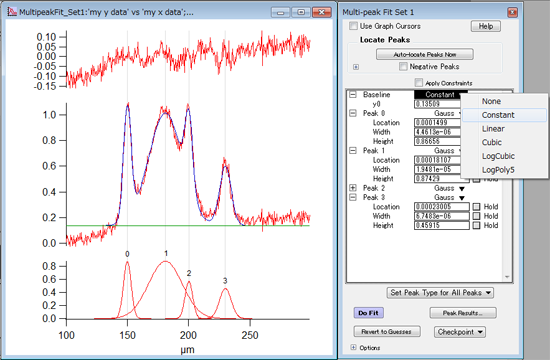
Here's an example of the plot I use to analyse my data ( UT4 vs. I have a large data set composed of several "independent" data frames like this one Tiempo UT1 UT2 UT3 UT4 UT5 UT6 UT7 UT8 UT9


 0 kommentar(er)
0 kommentar(er)
